Important new knowledge that instrument makers are discovering comes from engineers and scientists.

Modal analysis of a Guarnerius del Gesu 1728 at Johannsson Violins.
The fact is that scientific research has not succeeded in procuring the answer to the question of sound quality. However in the past few decades there has been an unbeleivably useful dialogue between acoustics researchers and the makers of musical instruments. It is safe to say that at no point since the classical age of italian violin making has there been a level of knowledge available to instrument makers as we are seeing today.
It is true that musicians and instrument makers with no formal knowledge of the technical aspects of their instruments, have a great capacity to get to the bottom of certain pressing questions by relying on their intuition and tacit knowledge gathered through experience. Lets not forget that the human being is still an infinitely superior processor of ideas than even the most sophisticated machine. Despite a considerable attempt by researchers for over 2 centuries to quantify and describe a fine violin tone, the tradition of empirical violin making is still the final contributor to excelence in violin tone. But nonetheless if we allow ourselves to see the computer as just another tool to help us understand things, there is no need for any ambiguity or conflicts about intuition and technology.
A distinction has to be made between knowledge of the way in which a thing behaves in physical terms and the way it sounds. A measurement of the response of an instrument in a graph is not the same thing as “a beautiful sound” The shape of a graph can be nice to look at but it isn´t sound.
The aesthetics of music and sound is one thing and measurements and observations are another.
Experimental Modal Analysis
A very powerful tool used by structural engineers is the technique of modal analysis. Every physical object vibrates at its own resonant frequencies determined by its mass stiffness and damping. Modal analysis maps the physical movement of objects for a range of frequencies. This is done by attaching a movement sensor called an accelerometer to the object and then then moving around with a so called impact hammer and hitting points on the object that conform to a grid or a matrix. The response can also be measured by velocity or displacement. In a simplified model of a periodic vibration shown below, the energy contained in the system alternates between momentum (a mass with velocity) and potential energy stored in the spring. At the extremities of displacement there is zero momentum and 100% stored spring energy. As the mass passes through rest position there is zero spring energy and maximum momentum. Imagine this as a representation of a point on the 2 dimensional diagram of a violin top (below), the point moving in the same way at 90 degrees to the surface of the plate.
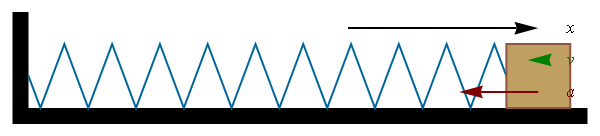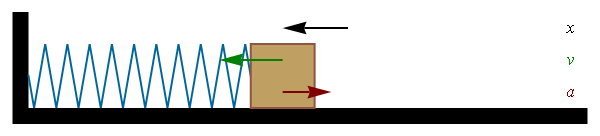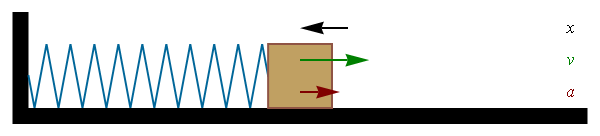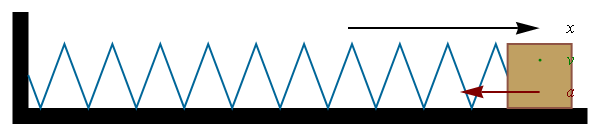
X is displacement,Y is velocity and A is acceleration.
A computer then calculates the amount of movement at each point on the grid. To measure the sound radiation and its directionality, an impact hammer strikes the bridge and measures the force, and a microphone positioned at various points in the room records the response, or frequency response function. An average of these measurements is then used to plot the spatial distribution of sound energy.
Among the techniques employed by some of today´s violin makers ,despite considerable apprehension by some, is experimental modal analysis, which was originally developed in the aerospace industries and psychoacoustic methodologies, which explore the way in which the ear and brain process sound.

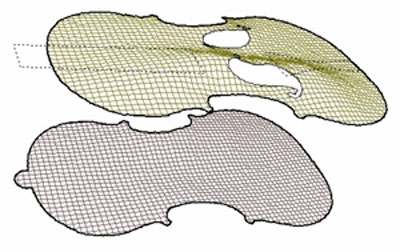
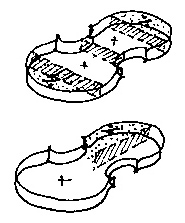
Stradivari violin analysed with an impact hammer in the studio for sound radiation, and a graphic representation of displacement at 540hz

This is a type of impact hammer used for modal analysis of bridges and other large constructions. This is useful for finding the eigenfrequencies, or normal modes of these structures.
This is a graphic representation of a real motorway bridge that has been modally tested.
The red and blue areas of this bridge show where the bridge reacted most strongly to the impact of the hammer.

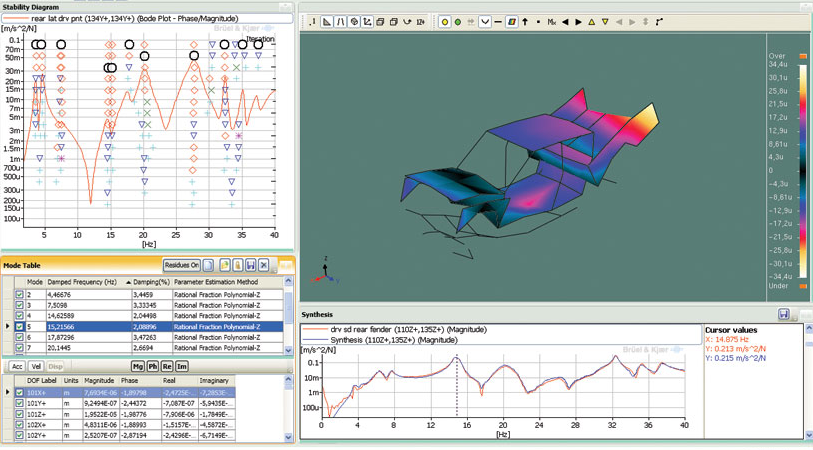
Modal analysis is used to generate useful data for the design of all kinds of structures from tiny equipment to large aircraft.
Through impact testing with a very sophisticated tiny hammer and a motion sensor, it has become practical in recent years to map the exact movements of the violin body at it´s main resonant frequencies. These motions and their characteristics, are directly related to the sound produced by the instrument.

A matrix of points on the surface of the instrument is mapped out and each point gets a small impact which records the response in each place. So some points will be stiffer and less able to move than others.

Finally the software renders a map of nodes and antinodes and the level of deflection at particular frequencies.
Software: Acquisition by George Stoppani
Modes
The sound quality of any instrument is mostly determined by its normal modes. Modal behaviour is simply the way a physical object reacts and deforms when it resonates.
Modes are simply the way in which objects vibrate at a particular frequency, how strongly they vibrate, and how damped they are. If they were undamped they would continue vibrating forever. A vibrating string displays different modes of vibration corresponding to each of its harmonic partials. Usually when a string is excited, its various modes will vibrate all at once as a conglomerate. A plate will also vibrate at its own "eigenfrequencies" and usually all the modes will be present at the same time, but varying in their strengths. Taking this a step further, the air mass inside an instrument also vibrates at its own frequencies. Also the whole body of an instrument will behave as one object and therefore contribute its own set of modes.
The normal modes of violins violas and cello´s etc. number in hundreds, but the one´s that are of greatest interest are the ones that radiate the most sound into a space. There are some modes which involve twisting and bending of the whole violin/neck body as a whole at low frequencies, but they do not radiate much sound. These low frequency modes can affect the way that an instrument feels like in the hands of the player though, as they cause an appreciable vibration. The violin has strong "breathing modes" which are characterised by air moving in and out of the soundholes.

The frequency response curves representing excellent instruments, show strong responses at approx. 270-280hz, which is caused by the lowest air resonance , 450hz and 550hz approximately, caused by the two main "breathing" body modes, and a peak at between 2500-3000hz which results mainly from localized wood bending modes in an area around the soundpost and bridge.
These important physical behaviours of the violin body are measured and plotted with various techniques.
Through impact testing with a very sophisticated tiny hammer and a motion sensor, it has become practical in recent years to map the exact movements of the instrument body at it´s main resonant frequencies. These motions and their characteristics, are directly related to the sound produced by the instrument.
The way in which the radiated sound waves are affected by the space the are contained in, can also be mapped and taken into consideration.
A model can then be made of the way in which the human ear and brain tend to respond to these physical stimuli.
First of all it might be a good idea to introduce the notion of modes of vibration, by making an analogy with the string . After all the behaviour of the string itself is very familiar to anyone who plays a stringed instrument.
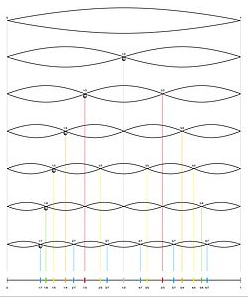

The bowed string vibrates at its lowest possible frequency as dictated by its length, its weight and tension, creating a series of overtones that are more or less multiples of the lowest tone.
That is- 1:2 would be the octave, 2:3 would be the fifth and so on.
We could think about the string in terms of its potential effect as simply its length and weight in addition to the amount of its deflection.
Now lets take that principle and switch it over to the next dimension which would be length, width and the amount of deflection or amplitude. This would be analogous to the vibration of the plates –back and front of the instrument.
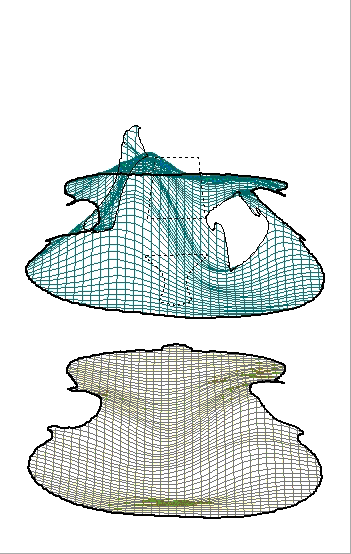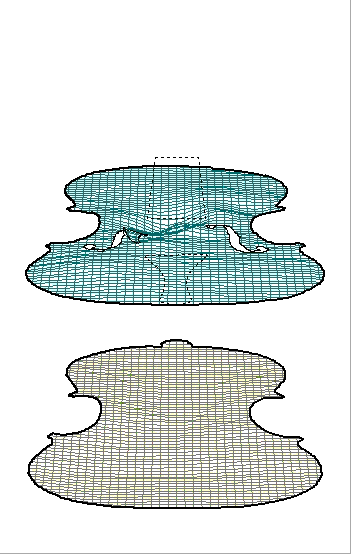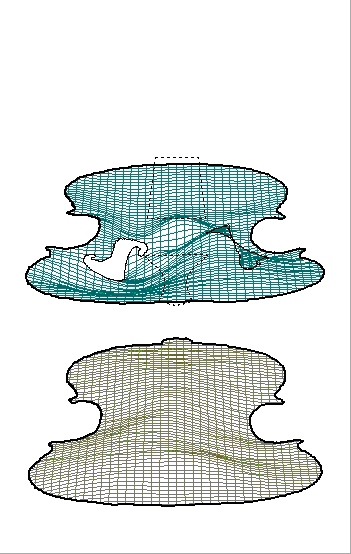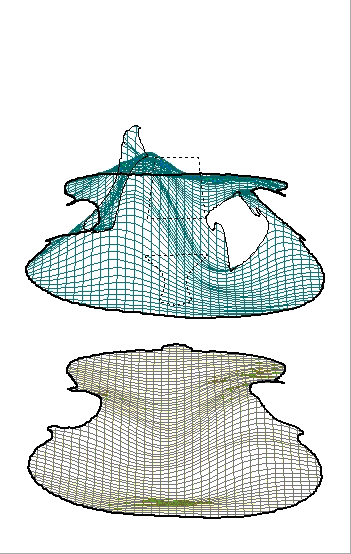


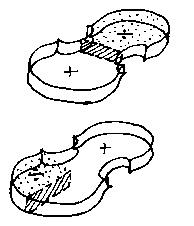
Stradivari violin,back and front (see above) at 540Hz
As we can see here plates tend to break up into segments of deflection with immobile areas in between , much like the string itself , except with one added dimension ,but because of the uneven shape and the different nature of the wood in one direction compared to the other, the plates dont break up into overtones that are neccessarily multiples of the lowest tone.



Acquisition plots of 357hz, 540hz and 2680hz respectively.
Red and blue are in opposite phase (Red is moving out while blue moves in)
Basically the higher the notes (or higher the frequency) that the plates are vibrating at, the smaller and more numerous the areas of vibrations that the plate is being split into. Whereas the lower notes split the plate into larger areas of movement.
The bowed stringed instruments amplify the almost inaudible vibrations of the strings themselves by two interdependent means:
One is the resonant vibrations of the wooden box itself .
The other is the resonant vibrations of the air enclosed in the box.
The wood resonances and the air resonances also couple or influence each other, because these two forms of energy are in direct contact. This makes the way in which a stringed instrument vibrates all the more complex.
Jumping from two dimensions to the third, we can begin to think about the vibrational behaviour of the enclosed air of our instrument.
The vibrations of the air inside the instrument are dictated by three factors:
1. The volume of the space inside.
2. The flexibility of the surrounding wooden box.
3. The size and thickness of the soundholes.
The air can be thought of in the same way as the strings and the plates in that it also breaks up into smaller and smaller sections of vibrations, with immobile areas or so-called nodes in between, except that now it is a question of various amounts of air pressure within a 3 dimensional enclosure.
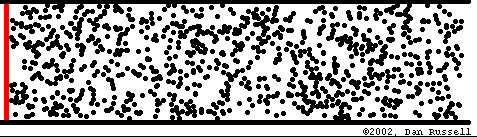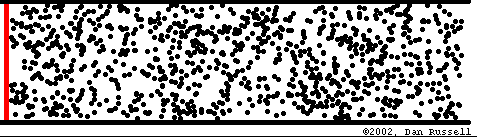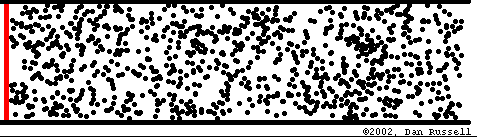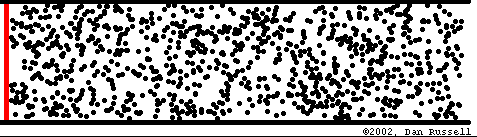
Animation representing the rarifications of an air mass in an enclosure,from Dan Russel´s web site.
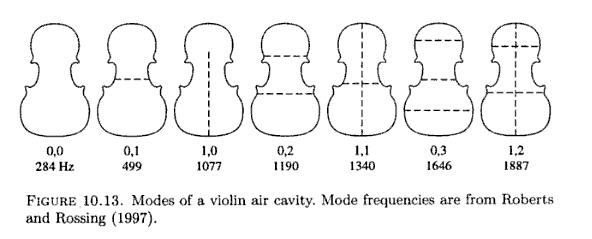
Maxima and minima of air modes.
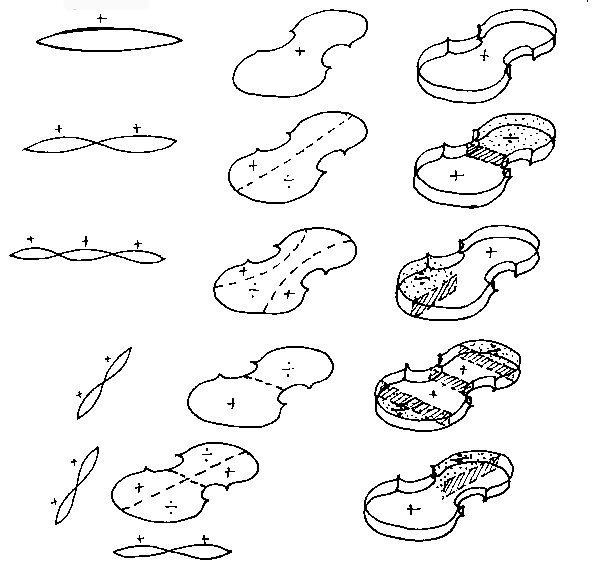
Here we see a summary of the modal behaviour of strings,plates and air volumes and what they have in common.
When the instrument is assembled as a whole it acts as a conglomorate of these different ways of vibrating, and at each natural wood and air resonance or their coupling, strengthens any note being played near them.
What all this means is that the input from the string is being strengthened at those particular notes that are near the instrument´s own resonances. By the instruments own resonances we mean the sounds produced by the instrument without the influence of the strings when it is made to vibrate with a knock for example.
Now, of the many modes of vibration that the instrument kicks into at different frequencies, only some are radiated as sound. Others radiate very little sound away from the instrument, but can nonetheless affect the way the string vibrates, by draining energy and producing little other than heat. . One of the resonances that don´t produce much sound is one that´s very easy to find and in fact if you don´t have perfect pitch, can be a great way to find the correct tuning for your instrument. On the violin or viola it can be found by holding the instrument vertically ,damping the strings and tapping lightly at the back of the scroll. It is like having an inbuilt tuning fork with you all the time. (the changes due to atmospheric conditions are very slight)
Of the modes of vibration that really produce sound, there are curiously very few. And so the actual response of a violin family instrument is not very even at all. The makers of loudspeakers and microphones try to get the response to be flat- in other words to make the response equally strong at all frequencies. But the violin family instruments do not respond equally at all. What we call an even sounding instrument is simply one that has the spacing of its resonances distributed so that each one strengthens a fairly broad range of notes. But as the frequency increases, there are more resonances and they are more tightly packed together, so it is really more the lower resonances that need to be strategically spaced.
You can find a few of your instruments main resonances by tapping lightly in a few places. You might also play the instrument at those pitches and see if you can get a feel for how those resonances are affecting the whole sound, but the fact that the instruments are not responding quite evenly also has some interesting consequences, especially in the higher frequencies. When you modulate a note by the use of vibrato –that note along with its row of overtones, is overlapping peaks of the instruments own response, back and forth, which of course creates a dramatic and very dynamic effect, which doesn´t happen when you play an electric violin, which has a fairly even response (like a microphone). Now this is one example where an apparent limitation (uneven resonance response) can be the medium for increased possibilities of creative expression.
The main resonances that contribute to sound radiation are to be found at different frequencies for each and every instrument of course, but they can be found in more or less similar ranges in violins violas ,cellos and double basses. Lets have a look at the placement for the average instrument.
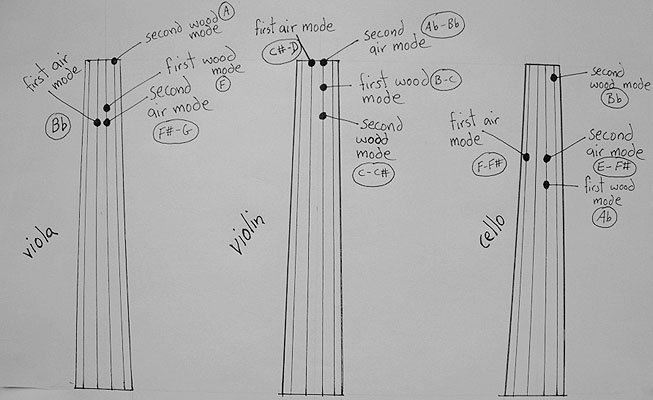
In the violin the main wood resonances are to be found at approximately A-Bb 440-to 550hz and B-C# ( ) and the main air resonances at C-D (275)and A-B(440-)
In the viola the main wood resonances are around F 350 hz and Ab-A 440 The main air resonances are Bb 230 hz and E-F# 330-360hz.
In the cello the main wood resonances are at approx. Ab and Bb and the main air resonances at E-F# and E-F# Of course this varies between instruments and can only be regarded as approximations.
In the violin, those main air and wood resonances help to strengthen the notes found at the lower end of the g-string by amplifying the second harmonic of the lowest tones and giving the impression of a stronger tone lower than what the instrument can really produce. This has to do with psychoacoustics, which is the psychology of perception as applied to hearing.
Psychoacoustics can show that we perceive a strong fundamental that is weak or doesn't exist due to the way the brain processes the harmonic series.
In the violin this is exemplified by the lowest tones on the g-string being strenghtened by a resonance that is really an octave higher than the lowest possible parts of its makeup. Lets look at an example:
The octave above the low A on the g-string of a violin is strenghtened by one of the body resonances and therefore gives the impression that the note is stronger than it really is. The fact that that tone is perceived as very strongly radiated has to do with the way the ear and the brain process sounds. The principles of psychoacoustics make it possible for a sound to be perceived as very well amplified even though the fundamental or lowest part of the sound is absent.
This can be shown by example in the following way.
Lets listen to a recording of a viola "Eb" with and without its lowest component and the spectrum of its fundamental note and its harmonics.
First we hear a viola “Eb”played normally,with and without vibrato.
And then the same tone, with and without vibrato,except here the lowest tone has been removed by computer filtering.
Considering the information that has been removed, it is extraordinary how the perception of the sound is retained, and we can easily draw an analogy to the visual parallel mentioned earlier, featuring the graphic image of the dog.
This has a lot to do with the discussion of viola size.
There are without doubt violas that are fairly small, that can sound very big. And often big violas feel more resonant to the player holding them than the audience listening actually hear. In fact for a viola to be able to produce fundamental amplification of its lowest tones it would have to be very large indeed.
A0
Usual abbreviation for the "air mode" of a violin or other instrument. This mode is a Helmholtz resonance, involving air flow in and out of the f-holes, but modified by the fact that the walls of the box are not rigid so that some breathing motion of the box also occurs. A0 is usually found around 280 Hz in a violin.
A1
Label for the second "air mode" of a violin. The mode is an "organ pipe" standing wave, with approximately a half-wavelength fitting into the length of the body cavity. It is usually around 480 Hz in a violin. It has a nodal line near the bridge, and is therefore not driven very effectively by the strings.
Accelerometer
Device for measuring vibration of a structure, producing an output signal proportional to acceleration. They work by having some kind of force-measuring sensor, with a mass attached to it so that when the device is forced to vibrate a force is produced by Newton's law, proportional to acceleration. There are two types: the force measuring element can be either a piezoelectric crystal or a cantilever beam fitted with a strain
gauge.
B0
Usual name for a low-frequency resonance mainly determined by a cantilever motion of the projecting piece of the fingerboard. It typically falls at about the same frequency as the air resonance A0. There is a school of thought that adjusting the frequency of B0 to be close to matching that of A0 is a good thing.
B1- B1+
Usual names for two strong resonances of a violin body, responsible for a lot of the sound radiation at low frequencies. Between them they are responsible for what older literature called the "main body resonance". Other labels for these modes are P1 and P2, or T1 and C3. For a violin, B1- is typically found around 450-480 Hz, B1+ around 530-570 Hz.
CBR
Acronym for a vibration mode of the violin body, coined by Bissinger: "C bouts rhomboidal". This is a mode usually in the general vicinity of 400 Hz for a violin, which shows up in input admittance measurements but is not a strong radiator of sound. This mode was labelled by Jansson "C2", and by Marshall "Vertical translation of C bouts".
Chladni pattern
Traditional way to visualise a vibration mode shape (or more properly, an ODS) by forcing the system to vibrate and then sprinkling powder such as sand or tea leaves on the surface. The powder collects at nodal lines.
Damping
“Damping” describes how quickly the energy in a vibration is dissipated. It is easiest to think about the response to tapping an object: there is an initial sound which dies away with time, fast if the damping is high and slow if the damping is low. If the vibrating structure is being driven in more-or-less steady vibration, as in a violin, then damping has a different consequence. It determines how strong the resonances of the structure are. If damping is low, a resonance will respond with a much bigger amplitude to a given level of excitation. As damping increases this resonant enhancement gets less, until if damping is too high there is no “resonance” at all.
Damping comes from many sources, which can be broadly grouped into three types. (1) “Material damping” describes energy loss due to “internal friction” within the body of the material the structure is made of. (2) “Boundary damping” describes energy loss associated with joins between different pieces of a structure: for example at a bolted join in a metal structure, there may be some frictional rubbing between the parts, or pumping of air in and out of small gaps. (3) Viscous and radiation damping. The structure is surrounded by air. Some energy is lost because it is carried away as sound waves. Some is also lost to viscosity of the air because of the local air flow around the edges of the structure.
Variation in material damping is one of the important factors in the difference between strings of different materials, or between different wood specimens.
Decibel
The decibel is a unit of level, used to describe for example loudness of sounds. It is a measure based on logarithms, and it describes the RATIO between two signals. 20dB is defined to be a factor of 10 in amplitude. 6dB is approximately a factor of 2. When decibel numbers are quoted, they are relative to some agreed reference level.
FFT
Acronym for "Fast Fourier transform". This the method used by a computer program to convert a recorded time signal into a frequency spectrum.
FRF
Acronym for "frequency response function". Related to "spectrum", also known as "transfer function". If you apply a force to a structure and measure the response somewhere (on the structure or with a microphone in the air) the FRF is a response per unit input force, as a function of frequency. It will have peaks at the resonances.
Hz
Abbreviation for Hertz, unit of frequency - "cycles per second". Named after 19th century German scientist.
Input admittance
A commonly-measured FRF for a violin: the velocity response at a string notch on the bridge to a force applied at the same point. Usually, the force and response would be aligned in the bowing direction. For practical reasons, input admittance is usually measured approximately, by applying the force to one corner of the bridge and measuring response on the other corner. An alternative name is "driving-point mobility".
Nodal line
A nodal line marks out the positions on a vibrating structure where a particular vibration mode is NOT vibrating. These lines separate regions where (at a given moment) the structure is moving in positive and negative directions.
Normal mode
A normal mode (or "eigenmode", or just "mode") is a pattern of vibration of a structure which corresponds to an individual resonant frequency (or "natural frequency", or "eigenfrequency"). Once the system is started off vibrating with one particular mode shape it will continue in that shape, oscillating at the corresponding natural frequency and gradually dying away because of the effect of damping. Any possible vibration of the system can be described as a mixture of the normal modes, each responding independently to the applied force. Mode shapes can be deduced from Chladni patterns, or more high-tech measurements such as laser holographic methods or "experimental modal analysis".
ODS
Acronym for "operating deflection shape". This is the pattern of response which you see if the structure (violin body or whatever) is driven with a sinusoidal force at a particular frequency. The ODS pattern will change as the frequency changes. Near a resonance, the ODS will be roughly the same as the mode shape, but not exactly the same because it will contain contributions from all the other modes as well.
Q value
A way to measure and describe the level of damping for a given vibration mode: high Q means low damping and conversely. The Q stands for "quality", because in the world of quartz crystal oscillators, a "high quality" oscillator has very low damping. The Q factor relates to the number of cycles it takes for the vibration to decay by a given factor.
Spectrum
Description, for a function of time, of the resolution of a signal into components, each of different frequency and (usually) different amplitude and phase.
Transient
A rather broad term, covering any aspect of sound or vibration which is not a steady periodic response. There are two main types of "transient" relevant to violins. The motion of the string in response to a bow gesture will go through some kind of transient before (usually) settling into the preferred Helmholtz motion. The nature and length of that transient are a big part part of judging the skill of the player, as well as of the sound. The second type of transient is the response of the violin body to some change in what the string does. The body resonances take time to build up or to die down following a change in excitation. This type of transient is most familiar through the "body knock" sound when you tap on the corner of the bridge. Recognition of a particular instrument (as opposed to a particular player) probably depends a lot on these transient sounds, which are unique to each instrument body.